Research
Method of Dimensionality Reduction (MDR)
MDR is a new method of simulation of contact and frictional forces between elastic and viscoelastic solids. MDR is simple in application, easy to learn and does not need any special knowledge in contact mechanics. Numerical implementation of MDR is almost trivial and allows to integrate the direct simulation of frictional contacts in finite elements or multi-body programs.
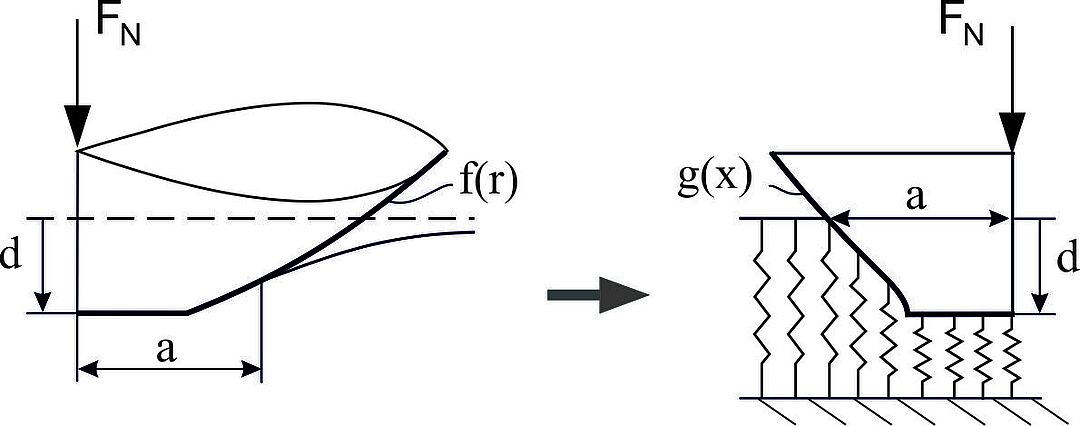
The MDR is based on the observation that close analogies exist between certain types of three-dimensional contact problems and the simplest contacts with a one-dimensional elastic foundation (Fig.). Thereby, it is important to emphasize that this is not an approximation: The properties of one-dimensional systems coincide exactly with those of the original three-dimensional system, if the form of the bodies is modified and the elements of the foundation are defined according to the rules of the MDR. The following book is recommended as a practical guide to the MDR.
 © J.Starcevic
© J.Starcevic
 © IfM
© IfM
Publikationen
Basics of the method of dimensionality reduction
A short practical introduction of the application of MDR to axis-symmetrical contacts:
Popov V.L., Hess M.: Method of dimensionality reduction in contact mechanics and friction: a users handbook. I. Axially-symmetric contacts, Facta Universitatis, series Mechanical Engineering, 12 (1): 1-14, 2014, pdf
A comprehensive treatise, including all necessary proofs:
Popov V.L., Hess M.: Method of dimensionality reduction in contact mechanics and friction, Springer 2014
A lecture on the MDR at TU Berlin:
A lecture on MDR by Prof. Popov held at the TU Berlin (130 min, in German),
English Translation of this lecture can be seen here
A lecture on the MDR on International friction forum:
A lecture on the MDR on International friction forum (115 min)
Two Review papers on MDR:
Popov V.L.: Basic ideas and applications of the method of reduction of dimensionality in contact mechanics. - Physical Mesomechanics, 2012, v. 15, N. 5-6, 254-263. pdf
Popov V.L.: Method of reduction of dimensionality in contact and friction mechanics: A linkage between micro and macro scales. Friction, 2013, v. 1, N. 1, pp. 41-62. pdf
Early Publications on MDR
Sketch of general ideas for multi-scale modeling of friction including the first ideas of MDR:
Popov V.L. and Psakhie S.G.: Numerical Simulation methods in tribology - Tribology International, 40, 916-923 (2007), pdf
Initial ideas of application of MDR to rough surfaces (later better understood and corrected):
Geike T. and Popov V.L.: Reduction of three-dimensional contact Problems to one-dimensional ones. - Tribology International, 40, 924-929 (2007), pdf
Geike T. and Popov V.L.: Mapping of three-dimensional contact Problems into one Dimension. - Phys. Rev. E., 76, 036710 (2007), pdf
Simulation of friction in the simplest model case of a pure viscous medium:
Popov V.L., Filippov A.E.: Force of Friction between Fractal Rough Surface and Elastomer. - Tech. Phys. Lett., 36, pp. 525 -527 (2010), pdf
First rigorous proofs of the general applicability of MDR to axisymmetric normal contacts:
Heß M.: Über die exakte Abbildung ausgewählter dreidimensionaler Kontakte auf Systeme mit niedrigerer räumlicher Dimension, doctoral thesis, chapt. 2 & 3, (2010/2011), link
Verification of MDR
Derivation of MDR mapping rules for axisymmetric normal contacts with and without adhesion:
Heß M.: About the exact mapping of selected three-dimensional contacts on systems with a lower spatial dimension, doctoral thesis in german, chapt. 2 & 3, (2010/2011), link
Verification of MDR for normal contact of self-affine surfaces:
Pohrt R., Popov V.L., Filippov A.E.: Normal contact stiffness of elastic solids with fractal rough surfaces for one- and three-dimensional Systems. - Phys. Rev. E, 86, 026710 (2012), pdf
Pohrt R., Popov V.L.: Investigation of the dry normal contact between fractal rough surfaces using the reduction method, comparison to 3D simulations. - Physical Mesomechanics, 15, 275-279 (2012), pdf
Verification of MDR for normal contact of self-affine rough surfaces with a viscous medium:
Kürschner S., Popov V.L.: Penetration of self-affine fractal rough rigid bodies into a model elastomer having a linear viscous rheology, - Phys. Rev. E, 87, 042802 (2013), pdf
Verification of MDR for contacts of rough spheres:
Pohrt R. and Popov V.L.: Contact Mechanics of Rough Spheres: Crossover from Fractal to Hertzian Behavior, Advances in Tribology, 2013, 974178 (2013), pdf
Verification of MDR in a broad range of surfaces profiles (from "White noise" roughness to smooth Hertz`contact):
Pohrt R., Popov V.L.: Contact stiffness of randomly rough surfaces. Sci. Rep. 3, 3293 (2013); DOI: 10.1038/srep03293, pdf
Applications of MDR
Shakedown in oscillating rolling contact:
Wetter R., Popov V.L.: Shakedown limits for an oscillating, elastic rolling contact with Coulomb friction. International Journal of Solids and Structures, 51 930-935 (2014). pdf
Wetter R., Popov V.L. Influence of the alignment of load and oscillation on the frictional shakedown of an elastic rolling contact with Coulomb friction. Physical Mesomechanics, 17, 31-38 (2014). pdf
Fretting wear:
Popov V.L.: Analytic solution for the limiting shape of profiles due to fretting wear, Sci. Rep. 4, 3749 (2014); DOI: 10.1038/srep03749. pdf
Dimaki A.V., Dmitriev A.I., Chai Y.S., Popov V.L.: Rapid simulation procedure for fretting wear on the basis of the method of dimensionality reduction. - International Journal of Solids and Structures, 51, 4215–4220 (2014). pdf
Li Q., Filippov A.E., Dimaki A.V., Chai Y.S., Popov V.L.: Simplified simulation of fretting wear using the method of dimensionality reduction. Physical Mesomechanics 17, 236-241 (2014), DOI: 10.1134/S1029959914030102. pdf
Simulation of stick-slip drives with frictional contacts:
Teidelt E., Willert E., Filippov A.E., Popov V.L. :Modeling of the dynamic contact in stick-slip micro-drives using the method of reduction of dimensionality. - Physical Mesomechanics, 15, N.5-6, 287-292 (2012). pdf
Nguyen H.X., Teidelt E., Popov V.L., Fatikow S.: Dynamical tangential contact of rough surfaces in stick-slip microdrives: modeling and validation using the method of dimensionality reduction. Physical Mesomechanics, 17, 304-310 (2014). DOI:10.1134/S1029959914040079. pdf
Nguyen H.X., Teidelt E., Popov V.L., Fatikow S.: Modeling and waveform optimization of stick-slip micro-drives using the method of dimensionality reduction. Archive of Applied Mechanics, DOI:10.1007/s00419-014-0934-y Springer Link
Elastomer friction:
Li Q., Popov M., Dimaki A., Filippov A.E., Kürschner S., Popov V.L.: Friction Between a Viscoe-lastic Body and a Rigid Surface with Random Self-Affine Roughness, Physical Review Letters, 111, 034301 (2013). pdf
Popov V.L., Voll L., Li Q., Chai, Y.S. & Popov M.: Generalized law of friction between elastomers and differently shaped rough bodies. Sci. Rep. 4, 3750 (2014); DOI:10.1038/srep03750. pdf
Li Q., Dimaki A., Popov M., Psakhie S.G. and Popov V.L. : Kinetics of the coefficient of friction of elastomers. Sci. Rep. 4, 5795 (2014); DOI:10.1038/srep05795. pdf
Relaxation damping in oscillating contacts:
Popov M, Popov V.L. & Pohrt R., Relaxation damping in oscillating contacts, Scientific Reports, 5,16189 (1-9 pp) (2015). pdf
Influence of oscillations on friction:
Starcevic J., Filippov A.E.: Simulation of the influence of ultrasonic in-plane oscillations on dry friction accounting for stick and creep. – Physical Mesomechanics, 15, 330-332 (2012). pdf
Milahin N., Starcevic J.: Influence of the normal force and contact geometry on the static force of friction of an oscillating sample. Physical Mesomechanics, 17, 228-231 (2014), 10.1134/S1029959914030084. pdf
Acoustic emission in rolling contacts on rough surfaces:
Popov M., Benad J., Popov V.L., Heß M.: Acoustic Emission in Rolling Contacts. In: Method of Dimensionality Reduction in Contact Mechanics and Friction, Springer, 2014, 207-214. pdf
Impact of elastic bodies:
Lyashenko, I.A. & Popov, V.L.: Impact of an elastic sphere with an elastic half space revisited: Numerical analysis based on the method of dimensionality reduction. Sci. Rep. 5, 8479; DOI:10.1038/srep08479 (2015). pdf
Adhesive impact of elastic bodies:
I.A. Lyashenko, E. Willert, V.L. Popov, Adhesive impact of an elastic sphere with an elastic half space: Numericalanalysis based on the method of dimensionality reduction, Mechanics of Materials, 92, 155-163 (2016), doi: 10.1016/j.mechmat.2015.09.009, pdf
Further generalization of MDR
Application of MDR to heterogeneous media:
Popov V.L.: Method of dimensionality reduction in contact mechanics and tribology. Heterogeneous media, Physical Mesomechanics, 17, 50-57 (2014). pdf
Criticism of MDR (There is a public discussion about the region of validity of MDR.)
A critical discussion of the MDR:
Ivan Argatov: A discussion of the method of dimensionality reduction, J. Mechanical Engineering Science, 2015, DOI: 10.1177/0954406215602512, pdf
The main critical arguments by B.N.J. Persson et. al.:
Lyashenko A., Pastewka L., and Persson B.N.J.: Comment on ‘‘Friction Between a Viscoelastic Body and a Rigid Surface with Random Self-Affine Roughness’’, Phys. Rev. Lett, 111, 189401 (2013). pdf
Response to the criticism by Persson:
Li Q., Popov M., Dimaki A., Filippov A.E., Kürschner, S., Popov V.L. and Pohrt R.: Reply to the above Comment, Phys. Rev. Lett.,111, 189402 (2013). pdf
Detailed Response to the crtiticism by Persson:
Popov V.L.: Comment on ‘‘Contact Mechanics for Randomly Rough Surfaces: On the Validity of the Method of Reduction of Dimensionality’’ by Bo Persson in Tribology Letters , Tribol Lett, 2015.doi:10.1007/s11249-015-0608-0, pdf
